조경기능사 자격증 시험 대비
삼각 지형 면적 구하기 문제풀이
해론의 공식, 사인 공식, 코사인 공식
삼각 지형의 면적구하기가 시험에 나오기도한다. 삼각지형의 넓이(면적)를 구하는 조건은
기본 높이와 밑변을 알 때, 기본 공식
세 변의 길이를 알 때, 헤론의 공식
두변의 길이와 끼인 각을 알 때, 삼각함수 + 피타고라스정의 + 헤론의 공식
각각 적용하는 공식으로 풀 수 있다.
기본 공식은 높이 X 밑변 / 2로 구하는 것은 익히 알고 있는 것이다.
사인 공식은 높이를 구하여 면적을 구하는 것이고, 코사인 공식은 피타고라스의 정의를 기초로 하여 헤론의 공식을 포함한다.
헤론의 공식
삼각형의 세 변의 길이를 통해 넓이를 구하는 공식이다. 이 공식에 그대로 적용하면 높이를 따로 구할 필요가 없이 면적을 구할 수 있다. 토지의 면적을 구하는 데 편리한 공식으로써도 알려져 있다.
이 공식은 알렉산드리아의 헤론이 그의 저서 《Metrica》에서 증명을 써 놓았기 때문에 헤론의 공식이란 이름이 붙여졌다. 현재에는 공식이 아르키메데스에게서 비롯한 것이거나, 이전부터 알고 있었을 수도 있었으리라 보인다.

삼각형 ABC의 세 각 A, B, C 및 이들이 마주하는 변의 길이가 각 a, b, c 인 선분으로 이루어진 삼각형이 있을 때,
세 변의 (합 / 2)를 s 라 하고

면적을 S라 하면,

s
코사인 법칙(law of cosines)
삼각형의 세 변과 한 각의 코사인 사이에 성립하는 정리이다. 이에 따르면,
삼각형의 (두 변의 제곱합)에서 (사잇각의 코사인과 그 두 변의 곱의 2배)를 빼면, 남은 변의 제곱과 같아진다. 코사인 법칙은 삼각형의 두 변과 그 사잇각을 알 때 남은 한 변을 구하거나, 세 각을 구하는 데 사용될 수 있고 면적을 구할 수 있다.

삼각형 ABC의 세 각을 마주하는 변을 a, b, c

코사인 법칙을 통해 삼각형의 두 변과 그 사잇각으로부터 제3의 변을 구할 수 있다. 세 변의 길이를 구하게 되면 헤론의 공식에 적용하여 면적을 구할 수 있다.
사인 공식(law of sines)
일반적인 사인 공식을 그대로 적용하면 된다. sinA = 높이 h/b(높이/빗변)에서 높이를 구한다. 사인 법칙은 삼각형의 두 변과 그 사잇각을 알 때, 높이와 면적을 구하는 데 사용될 수 있다.
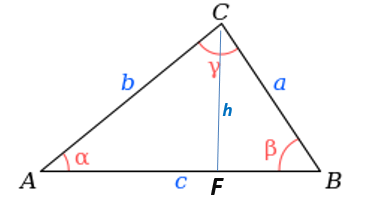
삼각형 ABC의 세 각을 마주하는 변을 a, b, c 라하면
sin(A) = h / b (높이/빗변)
cos(A) = b / c (밑변/빗변)
tan(A) = h / c (높이/ 밑변)
변 b의 길이와 변 c의 길이가 주어지고
그 끼인 각인 각 A의 값이 주어지면 sin 공식으로 높이를 구할 수 있고 이를 사용하여(밑변은 이미 주어졌다) 삼각지형의 면적을 구할 수 있다.
각 A의 값이 30도
변 b의 값이 60m이면, 높이(CF)는
sin(30) = 0.5
0.5 = h/60
CF(h) = 30m
■ 문제, 삼각형 X의 면적을 헤론의 공식으로

헤론의 공식으로(세 변의 길이 알 때)
헤론의 공식으로
길이 변수 s = (3 + 4 + 5) / 2
= 12 / 2
= 6
면적 S = √6(6-3)(6-4)(6-5)
= √36
= 6
기본 공식으로
3(밑변) x 4(높이) / 2
= 6
■ 문제, 삼각형 Y의 면적은?
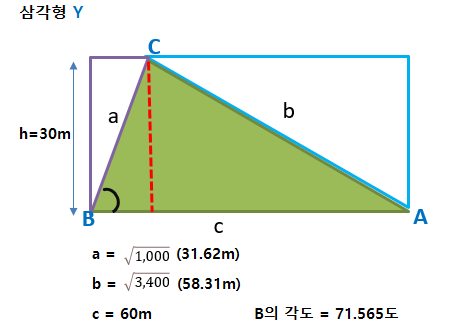
헤론의 공식으로(세 변의 길이 알 때)
헤론의 공식으로(세 변의 길이 알 때)
a = 31.62 , b =58.31 c =60 일 때
s = (31.62 + 58.31 + 60 ) / 2
= 74.965
s = 75로 보고
S = √ 75(75-31.62)(75-58.31)(75-60)
= 902.5㎡
기본 공식으로 (높이 알 때)
기본공식으로 (높이 알 때)
높이(30) x 밑변(60) / 2
= 900㎡
사인 공식으로(두변과 끼인 각을 알 때)
사인 공식으로(두변과 끼인 각을 알 때)
각, B = 71.565도
sin(71.565) = 0.9487
sin(B) = 높이/빗변 = h / 31.62
0.9487 = h/31.62
높이 = 0.9487 x 31.62 (√1000)
= 29.999
면적 = 밑변 x 높이 / 2
= 29.999 x 60 / 2
= 899.999
= 900㎡
코사인 공식으로(두변과 끼인 각 알 때)

코사인 공식으로(두변과 끼인 각을 알 때)
b의 길이를 모른다고 했을 경우
a = 31.62m, c =60m
각, B = 71.565도
cos(B) = 0.31623
c^2 = a^2 + b^2 - 2ab cos(B)
b^2 = c^2 + a^2 - 2ca cos(B)
= 3600 +1000 - (2 x 31.62 x 60 x cos(B))
= 3401
b = 58.31
헤론의 공식 적용
s = (31.62 + 58.31 + 60) / 2 = 74.96 = 75
S = √75(75-31.62)(75-58.31)(75-60)
= 902.5㎡
** 삼각형의 각도와 길이의 부정확성으로 오차가 발생함
■ 문제, 부등각 삼각형의 면적은?
두변과 끼인각이 주어졌을 때 (기출문제에 나옴)

면적을 사인 공식으로
Sin(40) = CD / 30
Sin(40) = 0.64278 = CD/30
CD(높이) = 0.64278 x 30 =19.2834
면적은 = 1/2(밑변 x 높이)
= 1/2( 20 x 19.2834 )
= 192.8㎡
면적을 코사인 공식으로
a = 30m, c =20m
각, B = 40도
cos(B) = 0.766
b의 길이 구하기
c^2 = a^2 + b^2 - 2ab cos(C)
b^2 = c^2 + a^2 - 2ca cos(B)
b^2 = (20)^2 + (30) ^2 - (2 x 30 x 20 x cos(40))
= 400 + 900 - 919
= 381
(b)^2= 381
b = 19.52
헤론의 공식 적용
s = (30 + 20 + 19.52) / 2 = 34.76
S = √34.76(34.76 - 30)(34.76-20)(34.76- 19.52)
= √34.76 x 4.76 x 14.76 x 15.24
= 192.92m2
단위용적 중량이 1700 kgf/㎥ 비중 2.6인 골재의 공극률은?
34.6%
질량 113kg의 목재를 절대 건조해서 100kg으로 되었다면 전건량 기준 함수율은?
13.00%
어떤 목재의 함수율이 50% 일 때 목재 중량이 3000g이라면 전건 중량은?
2000g
평판측량방법
평판을 고정하고 시준의를 사용
거리, 방향선, 고저 등을 측정하여 현장에서 제도
기록은 야장
수평 맞추기(정준, 정치)
중심 맞추기(구심, 치심)
방향 맞추기(표정) - 잘못 맞추면 가장 오차가 크다.
정구표, 정치표 - 평심방
■■
출처 : 이 사진과 글은 CC-BY-SA 3.0에 따라 공개 배포되는 위키백과 문서 를 사용합니다.
'기능사자격증으로 > 조경기능사 필기시험대비' 카테고리의 다른 글
| 조경기능사 필기대비 - 주요 수목의 종류 요약 (2) | 2024.01.24 |
|---|---|
| 조경기능사 필기시험 10일 합격 후기 (0) | 2024.01.22 |
| 조경기능사 필기대비 계산문제 풀이 (0) | 2024.01.20 |
| 조경시설물 관리 - 조경기능사 필기대비 (0) | 2022.06.23 |
| 화단, 실내조경관리 - 조경기능사 필기대비 (1) | 2022.06.22 |
| 조경관리, 잔디 관리 - 조경기능사 필기대비 (1) | 2022.06.22 |
| 조경관리, 수목 관리 - 조경기능사 필기대비 (1) | 2022.06.22 |



